Tính tổng các số chẵn, lẻ trong mảng 1 chiều lập trình C / C++
Chào các bạn đam mê lập trình! Hôm nay, tôi sẽ hướng dẫn các bạn cách tính tổng các số chẵn và số lẻ trong mảng một chiều sử dụng ngôn ngữ lập trình C/C++. Bài viết này sẽ giúp bạn hiểu sâu về cách xử lý mảng, điều kiện kiểm tra số chẵn lẻ và các kỹ thuật tối ưu trong lập trình.
Mục lục
- Giới thiệu về bài toán
- Phương pháp cơ bản để tính tổng số chẵn lẻ
- Sử dụng toán tử bitwise để tối ưu
- Tổ chức code với hàm
- Chương trình hoàn chỉnh với nhập liệu từ người dùng
- Phân tích độ phức tạp thuật toán
- Các ứng dụng thực tiễn
- Câu hỏi thường gặp
Giới thiệu về bài toán
Bài toán tính tổng các số chẵn và số lẻ trong mảng một chiều là một bài tập cơ bản nhưng rất quan trọng trong lập trình. Đây không chỉ là bài tập để rèn luyện kỹ năng xử lý mảng mà còn giúp hiểu về cách phân loại dữ liệu dựa trên điều kiện.
Số chẵn là số chia hết cho 2, số lẻ là số không chia hết cho 2. Việc tính tổng riêng cho từng loại số này thường xuất hiện trong nhiều ứng dụng thực tế như xử lý dữ liệu, thống kê và phân tích.
Để giải quyết bài toán này, chúng ta cần:
- Khởi tạo mảng một chiều
- Duyệt qua từng phần tử của mảng
- Kiểm tra mỗi phần tử là số chẵn hay số lẻ
- Cộng dồn vào biến tổng tương ứng
- Hiển thị kết quả
Phương pháp cơ bản để tính tổng số chẵn lẻ
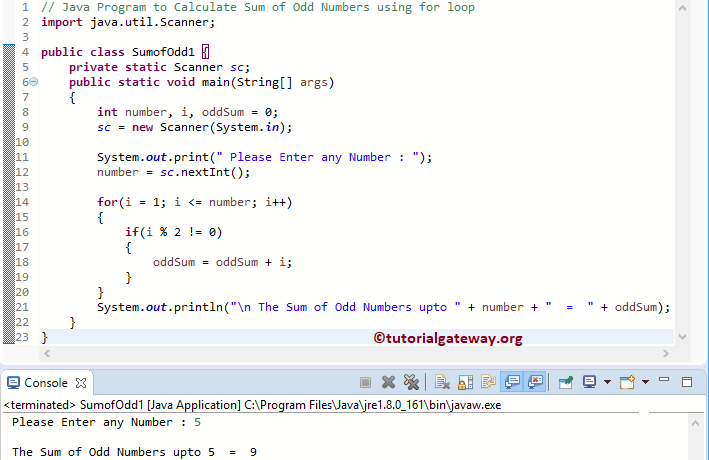
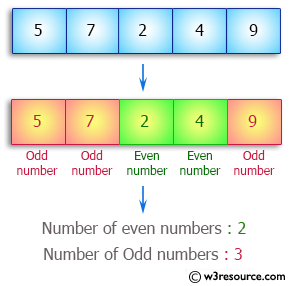
Cách thông dụng nhất để kiểm tra số chẵn lẻ trong C/C++ là sử dụng toán tử chia lấy dư (%). Một số nguyên là chẵn nếu chia cho 2 dư 0, và là lẻ nếu chia cho 2 dư 1.
Đây là đoạn code cơ bản để tính tổng các số chẵn và lẻ trong mảng:
cpp#include
using namespace std;
int main() {
int arr[] = {1, 7, 8, 4, 5, 16, 8};
int n = sizeof(arr)/sizeof(arr[0]);
int even_sum = 0, odd_sum = 0;
for(int i = 0; i < n; i++) {
if(arr[i] % 2 == 0) // Kiểm tra số chẵn
even_sum += arr[i];
else // Số lẻ
odd_sum += arr[i];
}
cout << "Tổng các số chẵn: " << even_sum << endl;
cout << "Tổng các số lẻ: " << odd_sum << endl;
return 0;
}
Trong ví dụ trên, chúng ta khởi tạo mảng arr[] với các phần tử cho sẵn. Sau đó duyệt qua từng phần tử và kiểm tra điều kiện số chẵn sử dụng toán tử %. Nếu số chia hết cho 2 (số chẵn), chúng ta cộng vào even_sum; ngược lại, cộng vào odd_sum.
Sử dụng toán tử bitwise để tối ưu
Một phương pháp tối ưu hơn để kiểm tra số chẵn lẻ là sử dụng toán tử bitwise. Phương pháp này thường nhanh hơn so với toán tử chia lấy dư, đặc biệt trên các hệ thống xử lý có hiệu suất thấp.
Nguyên lý: Nếu bit cuối cùng của một số là 0, số đó là chẵn; nếu là 1, số đó là lẻ. Chúng ta có thể kiểm tra bit cuối cùng bằng phép AND với 1 (& 1).
cpp#include
using namespace std;
int main() {
int arr[] = {1, 7, 8, 4, 5, 16, 8};
int n = sizeof(arr)/sizeof(arr[0]);
int even_sum = 0, odd_sum = 0;
for(int i = 0; i < n; i++) {
if((arr[i] & 1) == 0) // Kiểm tra số chẵn bằng bitwise
even_sum += arr[i];
else // Số lẻ
odd_sum += arr[i];
}
cout << "Tổng các số chẵn: " << even_sum << endl;
cout << "Tổng các số lẻ: " << odd_sum << endl;
return 0;
}
Phương pháp này thường được các chuyên gia tối ưu code sử dụng vì tính hiệu quả của nó trong xử lý bit.
Tổ chức code với hàm
Để code dễ bảo trì và tái sử dụng, chúng ta nên tổ chức nó thành các hàm riêng biệt. Dưới đây là cách cải tiến code bằng cách tạo một hàm chuyên biệt để tính tổng:
cpp#include
using namespace std;
// Hàm tính tổng số chẵn và lẻ
void calculateSums(int arr[], int size, int &evenSum, int &oddSum) {
evenSum = 0;
oddSum = 0;
for(int i = 0; i < size; i++) {
if(arr[i] % 2 == 0)
evenSum += arr[i];
else
oddSum += arr[i];
}
}
int main() {
int arr[] = {1, 2, 3, 4, 5, 6, 7, 8};
int size = sizeof(arr)/sizeof(arr[0]);
int evenSum, oddSum;
calculateSums(arr, size, evenSum, oddSum);
cout << "Tổng các số chẵn: " << evenSum << endl;
cout << "Tổng các số lẻ: " << oddSum << endl;
return 0;
}
Với cách tổ chức này, bạn có thể dễ dàng tái sử dụng hàm calculateSums trong các phần khác của chương trình hoặc trong các dự án khác. Đây là một thực tiễn lập trình tốt được khuyến nghị bởi các mẫu thiết kế phần mềm.
Chương trình hoàn chỉnh với nhập liệu từ người dùng
Để làm cho ứng dụng trở nên thực tế hơn, chúng ta sẽ tạo một chương trình cho phép người dùng nhập mảng:
cpp#include
using namespace std;
int main() {
int n;
cout << “Nhập kích thước mảng: “;
cin >> n;
if (n <= 0) {
cout << "Kích thước mảng không hợp lệ!" << endl;
return 1;
}
int *arr = new int[n]; // Cấp phát động bộ nhớ
cout << "Nhập " << n << " phần tử của mảng: ";
for(int i = 0; i < n; i++) {
cin >> arr[i];
}
int even_sum = 0, odd_sum = 0;
for(int i = 0; i < n; i++) {
if(arr[i] % 2 == 0)
even_sum += arr[i];
else
odd_sum += arr[i];
}
cout << "Tổng các số chẵn: " << even_sum << endl;
cout << "Tổng các số lẻ: " << odd_sum << endl;
delete[] arr; // Giải phóng bộ nhớ
return 0;
}
Chương trình này có thêm xử lý với các trường hợp đặc biệt như kiểm tra kích thước mảng hợp lệ và sử dụng cấp phát động bộ nhớ (new) để tạo mảng có kích thước do người dùng nhập. Đừng quên delete[] để tránh rò rỉ bộ nhớ!
Nếu bạn đang làm việc với các phần mềm đồ họa hoặc các ứng dụng xử lý ảnh, việc hiểu về xử lý mảng là rất quan trọng vì dữ liệu ảnh thường được lưu trữ dưới dạng mảng.
Phân tích độ phức tạp thuật toán ⏱️
Để đánh giá hiệu quả của thuật toán, chúng ta cần phân tích độ phức tạp thời gian và không gian:
- Độ phức tạp thời gian: O(n) – vì chúng ta cần duyệt qua tất cả n phần tử của mảng một lần duy nhất.
- Độ phức tạp không gian: O(1) – vì chúng ta chỉ sử dụng một lượng bộ nhớ cố định (biến đếm) bất kể kích thước mảng đầu vào.
So sánh với các phương pháp khác:
| Phương pháp | Độ phức tạp thời gian | Độ phức tạp không gian | Ưu điểm |
|---|---|---|---|
| Dùng toán tử % | O(n) | O(1) | Dễ hiểu, trực quan |
| Dùng toán tử bitwise | O(n) | O(1) | Nhanh hơn trên một số kiến trúc CPU |
| Dùng hàm đệ quy | O(n) | O(n) do stack | Code ngắn gọn nhưng kém hiệu quả |
Các ứng dụng thực tiễn
Việc tính tổng các số chẵn và lẻ trong mảng có nhiều ứng dụng thực tế:
- Xử lý ảnh: Trong Photoshop và các phần mềm đồ họa khác, việc xử lý riêng các pixel có tọa độ chẵn/lẻ có thể được sử dụng trong các bộ lọc đặc biệt.
- Mô hình hóa 3D: Trong 3DS MAX hoặc Autodesk Maya, nhiều thuật toán xử lý lưới sử dụng phân loại đỉnh chẵn/lẻ.
- Phân tích dữ liệu: Trong thống kê, việc phân tách và tính tổng dữ liệu theo các nhóm (như chẵn/lẻ) là một phần của phân tích mô tả.
- Thuật toán mã hóa: Một số thuật toán mã hóa xử lý riêng biệt các bit ở vị trí chẵn và lẻ.
Câu hỏi thường gặp ❓
1. Tại sao phải tính riêng tổng số chẵn và lẻ?
Việc phân tách và tính tổng riêng cho các số chẵn và lẻ giúp phân tích dữ liệu theo các nhóm đặc trưng, hữu ích trong nhiều bài toán thực tế như xử lý tín hiệu, phân tích thống kê.
2. Phương pháp nào hiệu quả hơn: dùng % hay bitwise?
Về mặt lý thuyết, toán tử bitwise nhanh hơn toán tử % vì nó hoạt động trực tiếp ở mức bit. Tuy nhiên, nhiều trình biên dịch hiện đại đã tối ưu hóa toán tử % nên sự khác biệt không đáng kể trong đa số trường hợp.
3. Làm thế nào để mở rộng bài toán này cho mảng nhiều chiều?
Với mảng nhiều chiều, bạn chỉ cần thêm các vòng lặp lồng nhau để duyệt qua tất cả các phần tử. Thuật toán cốt lõi vẫn giữ nguyên.
Ví dụ với mảng 2 chiều, bạn sẽ cần hai vòng lặp for lồng nhau để duyệt qua tất cả các phần tử. Điều này có thể áp dụng tương tự cho các ứng dụng AutoCAD khi xử lý dữ liệu lưới.
4. Có thể tối ưu thuật toán này hơn nữa không?
Đối với bài toán đơn giản này, thuật toán O(n) đã là tối ưu vì chúng ta phải kiểm tra mọi phần tử trong mảng. Tuy nhiên, nếu mảng được sắp xếp theo một cách đặc biệt hoặc có cấu trúc đặc thù, có thể có những tối ưu đặc biệt.
Kết luận
Bài toán tính tổng các số chẵn và lẻ trong mảng một chiều tuy đơn giản nhưng đã giúp chúng ta ôn lại nhiều khái niệm quan trọng trong lập trình C/C++ như: xử lý mảng, điều kiện, vòng lặp, tối ưu hóa và tổ chức code.
Đây là kỹ năng nền tảng cho nhiều bài toán phức tạp hơn trong xử lý dữ liệu, thiết kế đồ họa với Illustrator, chỉnh sửa ảnh với Lightroom và nhiều lĩnh vực khác.
Hãy thực hành code và thử nghiệm với các mảng khác nhau để hiểu sâu hơn về cách hoạt động của thuật toán này. Nếu bạn có thắc mắc hoặc cần hỗ trợ thêm, đừng ngần ngại để lại bình luận bên dưới nhé!
Chúc các bạn học tập và lập trình hiệu quả!
