Tính tổng bình phương các phần tử trong mảng C/C++ – Lập trình C – phanmemdohoa.com
Bạn đang tìm kiếm cách tính tổng bình phương các phần tử trong mảng bằng ngôn ngữ lập trình C/C++? Bài viết này sẽ hướng dẫn bạn chi tiết từ A-Z với những ví dụ cụ thể và giải thích dễ hiểu. Cho dù bạn là người mới học lập trình hay đã có kinh nghiệm, bài viết này đều mang lại giá trị cho bạn!
Mục lục
- Giới thiệu về phép tính tổng bình phương mảng
- Thuật toán tính tổng bình phương trong C
- Thuật toán tính tổng bình phương trong C++
- So sánh hiệu suất giữa các phương pháp
- Ứng dụng thực tế
- Các lỗi thường gặp và cách khắc phục
- Tối ưu hóa thuật toán
- Tổng kết
1. Giới thiệu về phép tính tổng bình phương mảng
Tính tổng bình phương các phần tử trong mảng là một bài toán cơ bản nhưng rất quan trọng trong lập trình. Phép toán này thường xuất hiện trong các thuật toán thống kê, xử lý tín hiệu, và nhiều lĩnh vực khác của khoa học máy tính.
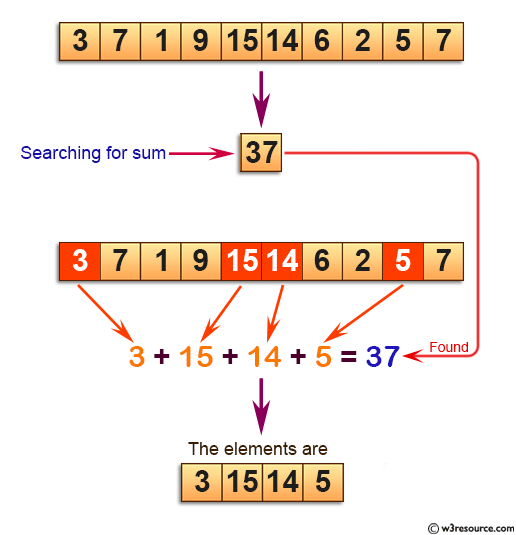
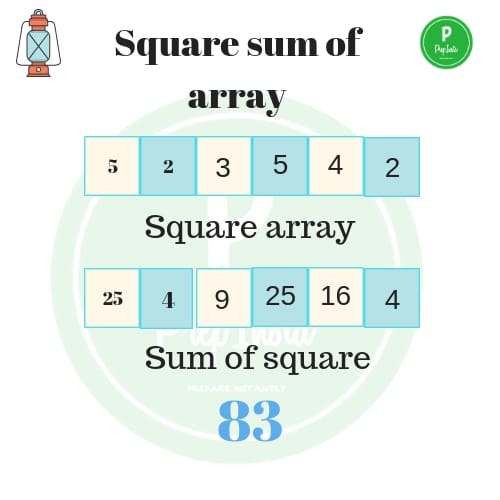
Tổng bình phương các phần tử là tổng của bình phương từng phần tử trong mảng. Ví dụ: với mảng [1, 2, 3, 4, 5], tổng bình phương sẽ là 1² + 2² + 3² + 4² + 5² = 1 + 4 + 9 + 16 + 25 = 55.
Phép tính này có nhiều ứng dụng thực tế như:
- Tính độ lệch chuẩn trong thống kê
- Tính khoảng cách Euclidean trong không gian vector
- Xử lý ảnh và tín hiệu số
- Các thuật toán học máy
2. Thuật toán tính tổng bình phương trong C
Dưới đây là cách triển khai cơ bản để tính tổng bình phương các phần tử trong mảng bằng ngôn ngữ C:
#include <stdio.h>
int main() {
int arr[] = {1, 2, 3, 4, 5};
int n = sizeof(arr)/sizeof(arr[0]);
int sum = 0;
for(int i = 0; i < n; i++) {
sum += arr[i] * arr[i];
}
printf("Tổng bình phương = %dn", sum);
return 0;
}
Giải thích chi tiết thuật toán:
- Khởi tạo mảng: Đầu tiên, chúng ta định nghĩa một mảng các số nguyên.
- Xác định kích thước mảng: Sử dụng biểu thức
sizeof(arr)/sizeof(arr[0])để tính số phần tử trong mảng. - Khởi tạo biến tổng: Biến
sumđược khởi tạo với giá trị 0. - Vòng lặp tính tổng: Duyệt qua từng phần tử của mảng, bình phương nó và cộng vào biến tổng.
- Hiển thị kết quả: In ra tổng bình phương các phần tử.
Với mảng {1, 2, 3, 4, 5}, kết quả sẽ là:
Tổng bình phương = 55
3. Thuật toán tính tổng bình phương trong C++
Cách triển khai cơ bản trong C++ tương tự như trong C, nhưng chúng ta sẽ sử dụng những tính năng của C++ để làm code dễ đọc và hiệu quả hơn:
#include <iostream>
#include <vector>
#include <numeric>
#include <functional>
using namespace std;
int main() {
// Cách 1: Sử dụng vòng lặp cơ bản
vector<int> arr = {1, 2, 3, 4, 5};
int sum1 = 0;
for(int i = 0; i < arr.size(); i++) {
sum1 += arr[i] * arr[i];
}
cout << "Tổng bình phương (cách 1) = " << sum1 << endl;
// Cách 2: Sử dụng range-based for loop (C++11)
int sum2 = 0;
for(int num : arr) {
sum2 += num * num;
}
cout << "Tổng bình phương (cách 2) = " << sum2 << endl;
return 0;
}
Trong C++, chúng ta còn có thể sử dụng thư viện STL để làm việc này một cách ngắn gọn hơn:
#include <iostream>
#include <vector>
#include <numeric>
#include <functional>
using namespace std;
int main() {
vector<int> arr = {1, 2, 3, 4, 5};
// Sử dụng STL transform và accumulate
int sum = accumulate(arr.begin(), arr.end(), 0,
[](int accum, int val) { return accum + val * val; });
cout << "Tổng bình phương = " << sum << endl;
return 0;
}4. So sánh hiệu suất giữa các phương pháp
Khi so sánh hiệu suất giữa các phương pháp tính tổng bình phương, chúng ta cần xem xét một số yếu tố:
| Phương pháp | Ưu điểm | Nhược điểm | Độ phức tạp |
|---|---|---|---|
| Vòng lặp for trong C | Đơn giản, dễ hiểu | Ít tối ưu | O(n) |
| Range-based loop trong C++ | Code ngắn gọn, dễ đọc | Chỉ có trong C++11 trở lên | O(n) |
| STL (accumulate + lambda) | Ngắn gọn, tận dụng thư viện chuẩn | Khó hiểu với người mới | O(n) |

Trong hầu hết các trường hợp với mảng có kích thước vừa phải, sự khác biệt về hiệu suất giữa các phương pháp là không đáng kể. Tuy nhiên, với mảng lớn, các phương pháp tối ưu hơn có thể mang lại hiệu quả rõ rệt.
5. Ứng dụng thực tế
Tính tổng bình phương các phần tử trong mảng có nhiều ứng dụng thực tế quan trọng:
5.1. Tính độ lệch chuẩn
Một trong những ứng dụng phổ biến nhất là tính độ lệch chuẩn trong thống kê:
#include <iostream>
#include <cmath>
using namespace std;
double calculateStandardDeviation(int arr[], int n) {
// Tính giá trị trung bình
double mean = 0.0;
for(int i = 0; i < n; i++) {
mean += arr[i];
}
mean /= n;
// Tính tổng bình phương độ lệch
double sumSquaredDiff = 0.0;
for(int i = 0; i < n; i++) {
sumSquaredDiff += pow(arr[i] - mean, 2);
}
// Tính độ lệch chuẩn
return sqrt(sumSquaredDiff / n);
}
int main() {
int data[] = {2, 4, 4, 4, 5, 5, 7, 9};
int size = sizeof(data) / sizeof(data[0]);
cout << "Độ lệch chuẩn: " << calculateStandardDeviation(data, size) << endl;
return 0;
}5.2. Tính khoảng cách Euclidean
Khoảng cách Euclidean giữa hai điểm là căn bậc hai của tổng bình phương hiệu các tọa độ tương ứng:
#include <iostream>
#include <cmath>
using namespace std;
double euclideanDistance(int point1[], int point2[], int dimensions) {
double sumSquared = 0.0;
for(int i = 0; i < dimensions; i++) {
int diff = point1[i] - point2[i];
sumSquared += diff * diff;
}
return sqrt(sumSquared);
}
int main() {
int pointA[] = {1, 2, 3};
int pointB[] = {4, 5, 6};
int dimensions = 3;
cout << "Khoảng cách Euclidean: " << euclideanDistance(pointA, pointB, dimensions) << endl;
return 0;
}
6. Các lỗi thường gặp và cách khắc phục ⚠️
Khi làm việc với việc tính tổng bình phương các phần tử trong mảng, có một số lỗi thường gặp mà bạn nên biết:
6.1. Tràn số (Overflow)
Vấn đề: Khi bình phương các số lớn, kết quả có thể vượt quá giới hạn của kiểu dữ liệu.
Giải pháp: Sử dụng kiểu dữ liệu lớn hơn như long long hoặc double:
#include <iostream>
using namespace std;
int main() {
int arr[] = {10000, 20000, 30000, 40000};
int n = sizeof(arr)/sizeof(arr[0]);
// Có thể gây tràn số với int
long long sum = 0; // Sử dụng long long thay vì int
for(int i = 0; i < n; i++) {
sum += (long long)arr[i] * arr[i]; // Ép kiểu để tránh tràn số
}
cout << "Tổng bình phương = " << sum << endl;
return 0;
}6.2. Truy cập ngoài mảng
Vấn đề: Truy cập vượt quá chỉ số mảng là lỗi phổ biến.
Giải pháp: Luôn kiểm tra giới hạn mảng:
// Đảm bảo i luôn nằm trong khoảng [0, n-1]
for(int i = 0; i < n; i++) {
// Code an toàn
}6.3. Lỗi với mảng rỗng
Vấn đề: Xử lý mảng rỗng không đúng cách có thể gây lỗi.
Giải pháp: Luôn kiểm tra mảng trước khi xử lý:
if (n > 0) {
// Thực hiện tính toán
} else {
cout << "Mảng rỗng!" << endl;
}7. Tối ưu hóa thuật toán
Dưới đây là một số cách để tối ưu việc tính tổng bình phương các phần tử:
7.1. Sử dụng Loop Unrolling
Loop unrolling là kỹ thuật tối ưu giúp giảm chi phí vòng lặp:
#include <iostream>
using namespace std;
int main() {
int arr[] = {1, 2, 3, 4, 5, 6, 7, 8};
int n = sizeof(arr)/sizeof(arr[0]);
int sum = 0;
// Loop unrolling - xử lý 4 phần tử mỗi lần lặp
int i = 0;
for(; i + 3 < n; i += 4) {
sum += arr[i] * arr[i] +
arr[i+1] * arr[i+1] +
arr[i+2] * arr[i+2] +
arr[i+3] * arr[i+3];
}
// Xử lý các phần tử còn lại
for(; i < n; i++) {
sum += arr[i] * arr[i];
}
cout << "Tổng bình phương = " << sum << endl;
return 0;
}
7.2. Sử dụng SIMD (Single Instruction Multiple Data)
Với các máy tính hiện đại, chúng ta có thể tận dụng các hướng dẫn SIMD để tính toán song song:
#include <iostream>
#include <immintrin.h> // Cho AVX
using namespace std;
// Lưu ý: Cần biên dịch với hỗ trợ AVX (ví dụ: -mavx với GCC)
int sumOfSquaresAVX(int* arr, int n) {
int sum = 0;
int i = 0;
// Xử lý 8 phần tử int cùng lúc với AVX
if (n >= 8) {
__m256i sumVec = _mm256_setzero_si256();
for (; i + 7 < n; i += 8) {
__m256i vec = _mm256_loadu_si256((__m256i*)(arr + i));
sumVec = _mm256_add_epi32(sumVec, _mm256_mullo_epi32(vec, vec));
}
// Gộp kết quả từ vector
int sumArray[8];
_mm256_storeu_si256((__m256i*)sumArray, sumVec);
for (int j = 0; j < 8; j++) {
sum += sumArray[j];
}
}
// Xử lý các phần tử còn lại
for (; i < n; i++) {
sum += arr[i] * arr[i];
}
return sum;
}⚠️ Lưu ý: Code SIMD trên đòi hỏi phần cứng hỗ trợ AVX và các tùy chọn biên dịch phù hợp.
8. Tổng kết
Trong bài viết này, chúng ta đã tìm hiểu chi tiết về cách tính tổng bình phương các phần tử trong mảng bằng C/C++. Từ các cách tiếp cận cơ bản đến các kỹ thuật tối ưu, bạn đã có đủ kiến thức để áp dụng thuật toán này vào các bài toán thực tế.
Tóm tắt những điểm chính:
- Thuật toán cơ bản trong C và C++ đều có độ phức tạp O(n)
- C++ cung cấp nhiều cách tiếp cận hơn với STL
- Cần chú ý các vấn đề như tràn số, giới hạn mảng
- Có thể tối ưu hiệu suất với loop unrolling và SIMD
Việc tính tổng bình phương các phần tử trong mảng là một kỹ năng cơ bản nhưng cực kỳ hữu ích trong lập trình C/C++. Hy vọng bài viết này đã giúp bạn hiểu sâu hơn về vấn đề này!
Bạn đang học lập trình C/C++ và muốn tìm hiểu thêm về các phần mềm đồ họa? Hãy khám phá thêm tại Phần mềm đồ họa - nơi chia sẻ phần mềm và tips đồ họa miễn phí, đã được xác minh 100%.
Các công cụ đồ họa liên quan có thể hữu ích cho bạn:
- Photoshop - Công cụ chỉnh sửa ảnh hàng đầu
- Illustrator - Phần mềm thiết kế vector chuyên nghiệp
- AutoCAD - Công cụ thiết kế kỹ thuật
Tham khảo thêm: Wikipedia - Sum of Squares, Moz - Algorithm Basics
